Ya os he hablado de Magnus Vigeland (ver https://parentela.familias.name/category/category4/). Pues bien, él ha desarrollado mucho software en R, y ahora Familias puede aprovecharse de ese trabajo!
Thore me ha enviado un ejemplo en el que se demuestra claramente el potencial que tiene combinar Familias y R. Podemos leer en R un archivo de Familias (.fam) con el comando «readFam», y también podemos dibujar los pedigríes definidos en el archivo de Familias con el comando «plotPedList».
Para poder hacerlo primero tenéis que saber dónde debe estar almacenado el archivo .fam para que R lo pueda leer. Para esto sólo tenéis que teclear en R:
getwd()
Y R os responderá dónde tenéis que almacenar el archivo .fam (también podríais indicar una ruta, pero es más fácil almacenar el archivo en el working directory de R).
Bueno, pues vamos a ver el ejemplo de Thore usando el archivo de familias sibs3.fam que podéis descargar aquí (ya sabéis, teclas Ctrl + S para descargarlo) y que debéis guardar en el working directory.
Ahora tenéis que instalar el paquete de R para aplicaciones forenses llamado «forrel». Para instalarlo sólo debéis teclear lo siguiente en Rstudio o en la consola R (se necesita conexión a internet):
install.packages(«forrel»)
La instalación de forrel sólo hay que hacerla una vez.
Ok, ahora ya estamos preparados para el ejemplo. Debéis teclear en R:
library(forrel)
x = readFam(«sibs3.fam», verbose = F)
plotPedList(x, marker = 1, shaded =
typedMembers, frametitles = names(x),
newdev = T, dev.width = 8)
Y en seguida veréis este resultado:
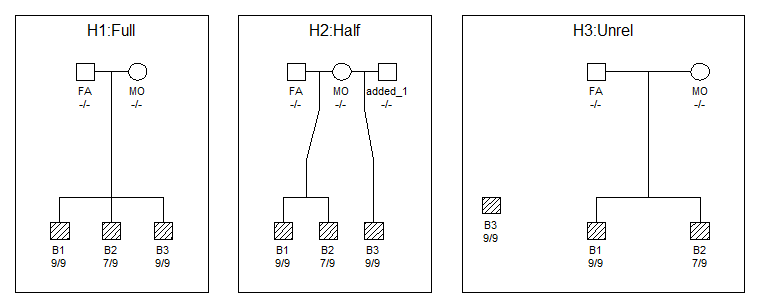
Maravilloso!! Muy útil para incluir los pedigríes en nuestros informes!!
También podemos calcular directamente los LRs en R si además tecleamos:
kinshipLR(x, ref = 3)
Y obtendremos:
## Total LR:
## H1:Full H2:Half H3:Unrel
## 8.333333 2.916667 1.000000
En el comando anterior, ‘ref = 3’ significa que los LRs están escalados con respecto a H3, es decir os da el LR con ‘H3:Unrel’ como referencia. Podéis encontrar más documentación y ejemplos si tecleáis:
?kinshipLR
Si decidís usar el working directory, cada vez que queráis usar esta herramienta con otro archivo, solo debéis modificar el nombre del archivo en las líneas de comandos de arriba:
En lugar de x = readFam(«sibs3.fam», verbose = F), debeis escribir x = readFam(«nombre de vuestro archivo.fam«, verbose = F)
O si preferís, en lugar de guardar el archivo .fam en el working directory de R, también podríais indicar la ruta en donde lo tengáis guardado, por ejemplo:
x = readFam(«C:/Users/lourditasmt/Documents/sibs3.fam», verbose = F)
Que rápido se hace y que bonito queda!!
Magnus y Thore, mil gracias, sois genios!!


