Como sabéis el LR no nos dice si una hipótesis es cierta o
no, más bien nos dice si nuestros resultados apoyan más una hipótesis que otra.
Por tanto, cuando decimos que:

a)
Si el LR > 1: los resultados apoyan H1 (la
del numerador)

b)
Si el LR = 1: la evidencia es neutra

c) Si el LR < 1: los resultados apoyan H2 (la
del denominador)

estamos hablando realmente en términos relativos, es decir
esto sólo es cierto en el caso de H1 con respecto a H2. Pero, qué pasa si hay
más escenarios posibles?, si hay más hipótesis?

Los que hayáis echado un vistazo a las diapos del curso de
enero que dieron Thore y Magnus en Oslo (y a las que tan amablemente Thore nos dio
acceso, ver cursos), sabréis la respuesta. Para los que no hayáis tenido tiempo de verlas, aquí
os reproduzco un ejemplo que, desde mi punto de vista, es buenísimo para
entender bien esto.

Imaginemos que analizamos los perfiles genéticos de dos
individuos y que queremos saber si pueden ser hermanos. Nuestras hipótesis
podrían ser: “H1 = hermanos” vs “H2: no relacionados”.

Imaginemos que tras el análisis hemos obtenido exactamente
el mismo perfil genético en los dos individuos. Si valoramos nuestra evidencia
teniendo en cuenta esas dos hipótesis, lógicamente el LR nos va a salir elevado, por ejemplo 10^6. La
evidencia por tanto apoya la hipótesis de que son hermanos, pero sólo cuando la
comparamos con la hipótesis de que no estén relacionados.

Obviamente, si descartamos un error en el lab (como podría
ser el hecho de haber analizado la misma muestra dos veces en lugar de analizar
las dos muestras), enseguida nos viene a la mente una tercera hipótesis: “H3=
gemelos idénticos”. Si ahora valoramos este resultado teniendo en cuenta las
hipótesis H3 y H2, el LR nos dará un número aún más elevado (imaginemos que
sale 10^15).

Consideremos ahora que a priori, las tres hipótesis tienen
la misma probabilidad (1/3 cada una). En la tabla siguiente (diapositiva 43 de
la charla “Forensics I: paternity cases, complex identification cases” de
Thore), podéis ver las probabilidades a posteriori:

Así que, en este caso, aunque el LR que obtenemos al tener
en cuenta H1 y H2 es mucho mayor que 1 (10^6), lo cierto es que la probabilidad
a posteriori (P (H1│E)) es menor que la probabilidad a priori (10^9 < 1/3).

Imaginemos ahora que damos mucha más probabilidad a priori a
las hipótesis H1 y H2, y una probabilidad a priori muy pequeña a H3; por
ejemplo casi 0.5 a H1 y H2, y sólo 10^(-6) a H3 (0.000001). Si calculamos las probabilidades
a posteriori, obtenemos (diapositiva 44 de la charla anterior):

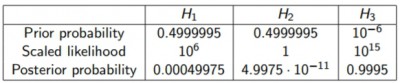
De nuevo, la probabilidad a posteriori de H1 es menor que su
probabilidad a priori. Y respecto a H3, a pesar de que hemos definido que su
probabilidad a priori sea muy baja, su probabilidad a posteriori es muy
elevada, ya que H3 es la mejor explicación de nuestros resultados.

Por tanto, aunque el LR que evalúa nuestros resultados comparando
H1 (hermanos) y H2 (no relacionados) es mucho mayor que 1, esto no significa
que H1 sea una buena hipótesis (o que H1 sea cierta). Perfectamente puede
significar que H1 no es una buena hipótesis y que H2 es aún peor. Lo dicho
entonces, que el LR no nos dice si una hipótesis es cierta o no.

En el siguiente post veremos cómo se han calculado las
probabilidades a posteriori en este ejemplo, y lo que podemos aprender de él.