Fechas de Cumpleaños y Blind Search – Parte 2

Queridos!
Lo primero de todo es desearos un muy feliz Año
Nuevo 2018. Espero que este año venga cargado de salud, amor, alegrías y…
muchos LRs!! No porque quiera que tengáis mucho trabajo, sino
porque espero que vuestro trabajo se vea recompensado con muchas
identificaciones (aunque tb podemos calcular LRs en casos de mismatch, como ya
sabéis)

Bueno, nos quedaba pendiente la parte dos del
comentario que me envió Thore sobre la relación entre la «paradoja del
cumpleaños» y la herramienta Blind Search. Como en la parte 1, os pongo
aquí mi traducción personal y el texto original en inglés a continuación.

Muchos de vosotros ya estáis familiarizados con la
herramienta Blind Search de Familias, así que sólo revisaremos la idea básica
necesaria para entender un ejemplo diseñado para ilustrar la “paradoja del
cumpleaños” y sus implicaciones forenses.

Consideremos un workshop al que asisten 50
participantes no emparentados entre sí, a los que llamaremos Alumno1,…,
Alumno50. Hemos genotipado a todos ellos, analizando un STR autosómico.
Imaginemos que este marcador tiene la siguiente propiedad:
si elegimos 2 individuos al azar, éstos serán idénticos para ese marcador (bien sean
ambos homocigotos o heterocigotos) con probabilidad 1/365.
Resulta que esto es cierto si el marcador elegido tiene los alelos 1, 2,…, 19
(es decir, 19 alelos distintos), cada uno con frecuencia 1/19. Los que estéis
interesados en saber por qué, podréis ver los detalles matemáticos más abajo;
los que no lo estéis, os lo creéis y ya está. En otras palabras, la
probabilidad de identidad genética se corresponde con la probabilidad de que
dos individuos tengan la misma fecha de cumpleaños.

Simulemos
genotipos para estos alumnos en Familias, seleccionando la opción “Save raw
data”. El archivo resultante puede leerlo Familias si usáis la opción “Import”
en “Tools > DVI module > Add Unidentified Persons” (introducir los datos
genéticos simulados manualmente no es recomendable). Los genotipos para los 22
individuos primeros son:

Después, desde esta misma ventana podemos hacer un Blind Search, y si
seleccionamos “Direct match” y los siguientes parámetros:
Obtenemos:

Como veis, hay 4 matches, y os detallamos el obtenido
entre los alumnos 2 y 19 (ambos heterocigotos 4-7). Sería una sorpresa no
obtener ningún match, ya que en la gráfica del cumpleaños del post anterior
veíamos que la probabilidad de obtener al menos 1 match era del 97% para 50
alumnos. Podemos también explicar este resultado de 4 matches: con 50 alumnos
hay (50*49)/2=1225 posibles comparaciones de pares de alumnos (combinaciones de
50 elementos, tomados de 2 en 2, si recordáis un poco la combinatoria). Por
tanto, se esperan 1225*(1/365) = 3.5 matches, muy cerca de los 4 matches que
obtuvimos en la simulación.

¿Que nos dice entonces la paradoja del cumpleaños y la
parte forense anterior? Pues que la opción Blind Search de Familias realiza
todas las comparaciones por pares posibles. El número de comparaciones es muy
elevado cuando hacemos la búsqueda con una larga lista de perfiles genéticos.
Si tuviéramos 1000 perfiles, habría 499500 ((1000*999)/2), aproximadamente
medio millón de comparaciones.

Con esta cantidad de comparaciones está claro que no
podemos ignorar la posibilidad de un match falso (como nos ocurre cuando
hacemos búsquedas en las bases de datos nacionales). El problema de la
valoración de un match obtenido tras la búsqueda en una base de datos se ha
discutido ampliamente en la literatura forense (ver por ejemplo Storvik and
Egeland, Biometrics, 2007). Una posible solución sería multiplicar los odds a
priori de un match por el LR, para obtener los odds a
posteriori, y así poder reportar este valor en el informe pericial. Pero,
también nos encontramos con el problema de que no es tan fácil alcanzar un
consenso sobre qué odds a priori usar.

Que curioso todo esto, ¿verdad? Nunca
se me hubiera ocurrido relacionar matches genéticos con fechas de cumpleaños…
Mil gracias Thore!!!

Detalles matemáticos:
Seleccionamos
un marcador con alelos 1,…,n; todos ellos con frecuencia 1/n. La probabilidad
de que 2 individuos al azar coincidan en sus genotipos es:

El LR, para un match directo de genotipos heterocigotos, como el que
obtuvimos entre los alumnos 2 y 19 con Familias, es:
El LR, para un match de «hermanos» de genotipos heterocigotos,
sería:

como podéis confirmar con Familias:

Lo que recibí de Thore:

Birthdays and Blind Searches. Part II

We
assume some familiarity with Blind search and only review the basic idea for an
example designed to illustrate the Birthday paradox and its Forensic
implications. Consider a class of of 50 unrelated pupils named Pupil1, …,
Pupil50. These pupils have been genotyped for one autosomal marker. This marker
has the property that two randomly chosen individuals are identical (homozygous
or heterozygous match) with probability 1/365 (**mathematical details are below
for those interested. It turns out that this can be achived by chosing a marker
with alleles 1,2, …, 19; all with frequencies 1/19). In other words, the
probability of genetical identity corresponds to the probability that two
individuals have the same birthday. We simulated marker data for these pupils
in Familias and ticked of the ‘Save raw data’ option. The resulting output file
was edited and read into Familias using the ‘Import’ option of ‘Tools > DVI
module > Add Unidentified Persons’. The marker data of the first 22
individuals are:

We next do a ‘Blind search’, select ‘Direct match’
and parameters as below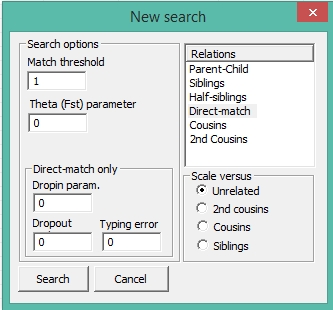

We get the following output:

There are four
matches, the one between pupils 2 and 19 is detailed. We would be very suprised
if there had been no matches as the birthday plot shows that the probability
for at least one match is 97% for 50 pupils. We can also add some further
intuition to this: With 50 there are 49*50/2 =1225 pairs of pupils that can
compare their birthdays. We expect 1225*(1/365)=3.5 matches; close to the 4
matches thissimulation gave.

What do we learn form the Birthday paradox and the forensic counterpart
illustrated above? The Blind search option performs all pairwise comparisons.
The number of comparisons becomes large when we search a large list of
profiles. For a list of 1000 profiles there are 499500 or roughly half a
million comparisons. Therefore, the risk of a false match cannot be ignored.
The problem of evaluating the evidence of a match found from a database search
has been widely discussed in the forensic literature (see eg Storvik and
Egeland, Biometrics, 2007). One possible solution is to multiply the prior odds
of a match with LR to obtain the posterior odds. This posterior odds can then
be reported. However, it may not be easy to reach a consensus on what prior
odds to use.

**Mathematical
details. We choose a marker with alleles 1,…,n; all with frequency 1/n. The
probability that two random individuals match is

The LR for an heterozygous match, as between pupils
2 and 19 above, is